Automating Feature Engineering in Supervised Learning

Automating Feature Engineering in Supervised Learning

Introduction

举了一个例子。通过用 $sin $ 进行映射，样本点可以被分组。

$\to$ 定义一个映射函数

举心脏病的例子,说明实际上真正重要的因素往往是几个主要因素的组合,如$ BMI $

New tech consider the selection of features as black boxes, and is drien by the actual performance.

$\to$ applying reinforcement learning

Challenges in Performing Feature Engineering

人工极大根据经验

强化算法也不需要经验

Terminology and Problem Definition

1. $F=\lbrace f_1,f_2,…,f_m \rbrace$

2. $A\ target\ vector\ y$

3. $A\ suitable\ learning\ algorithm\ L$

4. $A\ measurement\ of\ performance\ m$

5. $A_L^m(F,y)\ signify\ performance$

   for example, $L$ can be Logitic regression and m is cross entropy

6. $Assume\ a\ set\ of\ transformation\ function\ \lbrace t_1,t_2,…t_m \rbrace $

   $$ f_{out}=t_i(f_in)\ where\ f_{in},f_{out} \in R^n$$

define set of operations: $+$

aim: $$ F^*=argmax_{F1,F2}A^m_L(F_1 \bigcup F_2) \ F1\ from\ original\ dataset \ F2\ form\ derived\ dataset $$

A Few Simple Approaches

1. Apply all $Transformation\ Function$ to the given data and sum them up

   • Ad: Easy

   • Dd:computation inefficiency & overfitting

2. Every time add a new feature, train and evaluate

   • more scalable

   • Dd: also slow because the model training and evaluation

     refuce the deep composition of transforms

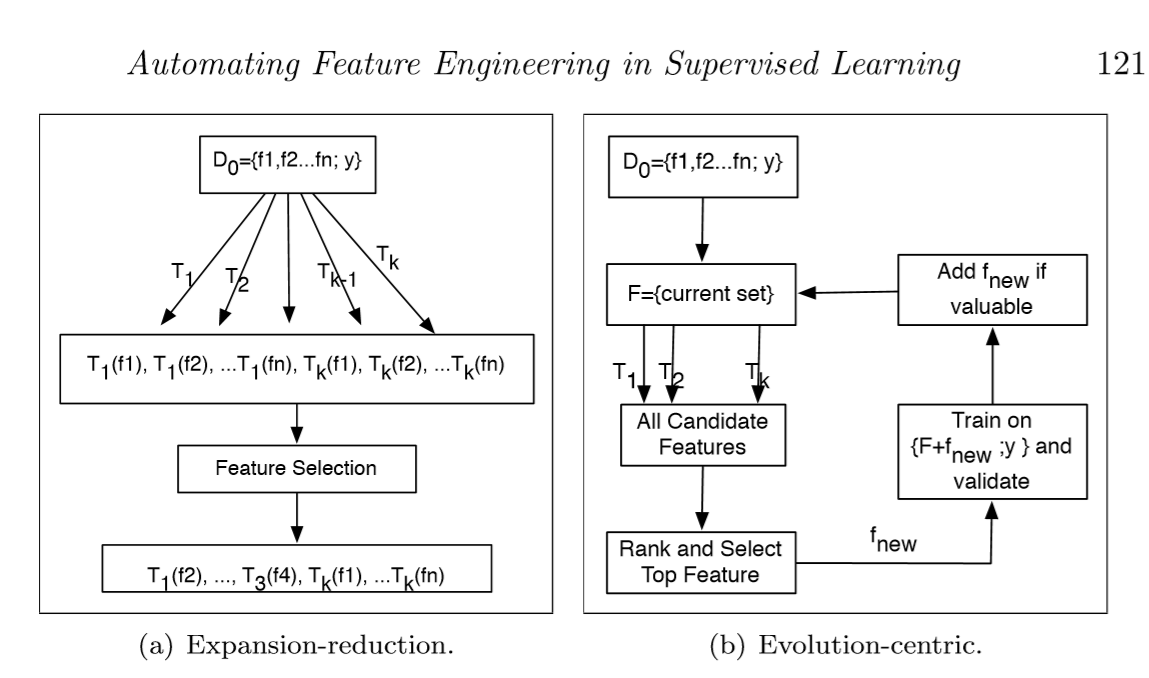
Hierarchical Exploration of Feature Transformations

idea: batching of new features & hierarchical composition

Transformation Graph

The transformation graph: $G$

Given Dataset:$D_0$

After each transformation, the target will not change

The node type:

• start
• from $T(D_{before})$
• from $D_1+D_2$

$\theta (G)$ refers to all nodes in $G$

$\lambda(D_0,D_1)$ refers to the transformation function $T$ makes $D_0 \to D_1$

the best solution is always among one of the nodes

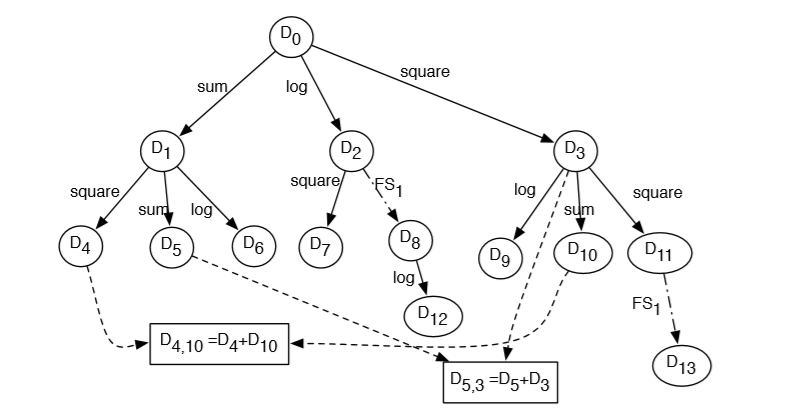
Transformation Graph Exploration

Dataset D_0, MAX_SEARCH_TIMES
# G_0 is start_gragh, D_0 is the start_dataset
# G_i refers to the graph after i-1 transformation
time =0
while time < MAX_SEARCH_TIMES:
    Nodes = θ(G_time)
    b_ratio = time / MAX_SEARCH_TIMES
    Nodes_plus,Transform_plus = argmax(n,t) Rank(G_time,Nodes,Transform,b_ratio)
    G_(time+1)=Apply Transform_plus on Nodes_plus
    time = time+1
 '''
 time can be any element through the exploration, like consuming time
 '''

Learning Optimal Traversal Policy

consider the reinforcement as Markov Decision

the state at step i is divided into two parts:

(a). $G_i$ after i node-addtions

(b).the remaining budget $b_{ratio}=\frac {i}{B_{max}}$

Let the entire set of states as $S$

an action at step i is$<n,t>$

$n$ is nodes to add while $t$ is transformation function in accord

To each step i, we get a reward $r_i$

$$ r_i =max_{n'\in\theta(G_{i+1})}\ A(n') - max_{n\in\theta(G_{i})}\ A(n)\ where\ r_0=0 $$ The cumulative reward over time from state $S_i$

$$ R(S_i)=\sum_{j=1}^{B_{max}} \gamma ^i \cdot r_{i+j} $$ We apply $Q-Learning$

$$ Q(s,c)=r(s,c)+\gamma(R)^\prod (\delta(s,c)) $$ The aim is:

$$ \prod^*(s,c)= arg\ max_cQ(S,C) $$

Give an approximate prediction:

$$ Q(s,c)=w^c \cdot f(s) \where f(s)=f(g,n,t,d) $$